Hausdorff distance
In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance,[1] measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right. It is named after Felix Hausdorff.
Informally, two sets are close in the Hausdorff distance if every point of either set is close to some point of the other set. The Hausdorff distance is the longest distance you can be forced to travel by an adversary who chooses a point in one of the two sets, from where you then must travel to the other set. In other words, it is the farthest point of a set that you can be to the closest point of a different set.
It seems that this distance was first introduced by Hausdorff in his book "Grundzüge der Mengenlehre" the first edition published in 1914.
Contents |
Definition
Let X and Y be two non-empty subsets of a metric space (M, d). We define their Hausdorff distance d H(X, Y) by
where sup represents the supremum and inf the infimum.
Equivalently
 ,[2]
,[2]
where
 ,
,
that is, the set of all points within  of the set
of the set  (sometimes called the
(sometimes called the  -fattening of
-fattening of  or a generalized ball of radius
or a generalized ball of radius  around
around  ).
).
Remark
It is not true in general that if  , then
, then
 .
.
For instance, consider the metric space of the real numbers  with the usual metric
with the usual metric  induced by the absolute value,
induced by the absolute value,
 .
.
Take
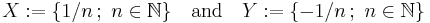 .
.
Then  . However
. However  because
because  , but
, but  .
.
Properties
In general, dH(X,Y) may be infinite. If both X and Y are bounded, then dH(X,Y) is guaranteed to be finite.
We have dH(X,Y) = 0 if and only if X and Y have the same closure.
On the set of all non-empty subsets of M, dH yields an extended pseudometric.
On the set F(M) of all non-empty compact subsets of M, dH is a metric. If M is complete, then so is F(M).[3] If M is compact, then so is F(M). The topology of F(M) depends only on the topology of M, not on the metric d.
Motivation
The definition of the Hausdorff distance can be derived by a series of natural extensions of the distance function d(x, y) in the underlying metric space M, as follows:[4]
- Define a distance function between any point x of M and any non-empty set Y of M by:
-
 .
.
- For example, d(1, [3,6]) = 2 and d(7, [3,6]) = 1.
- Define a distance function between any two non-empty sets X and Y of M by:
-
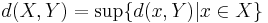 .
.
- For example, d([1,7], [3,6]) = d(1, [3,6]) = 2.
- If X and Y are compact then d(X,Y) will be finite; d(X,X)=0; and d inherits the triangle inequality property from the distance function in M. As it stands, d(X,Y) is not a metric because d(X,Y) is not always symmetric, and d(X,Y) = 0 does not imply that X = Y (It does imply that
 ). For example, d([1,3,6,7], [3,6]) = 2, but d([3,6], [1,3,6,7]) = 0. However, we can create a metric by defining the Hausdorff distance to be:
). For example, d([1,3,6,7], [3,6]) = 2, but d([3,6], [1,3,6,7]) = 0. However, we can create a metric by defining the Hausdorff distance to be:
Applications
In computer vision, the Hausdorff distance can be used to find a given template in an arbitrary target image. The template and image are often pre-processed via an edge detector giving a binary image. Next, each 1 (activated) point in the binary image of the template is treated as a point in a set, the "shape" of the template. Similarly, an area of the binary target image is treated as a set of points. The algorithm then tries to minimize the Hausdorff distance between the template and some area of the target image. The area in the target image with the minimal Hausdorff distance to the template, can be considered the best candidate for locating the template in the target.[5] In Computer Graphics the Hausdorff distance is used to measure the difference between two different representations of the same 3D object[6] particularly when generating level of detail for efficient display of complex 3D models.
Related concepts
A measure for the dissimilarity of two shapes is given by Hausdorff distance up to isometry, denoted DH. Namely, let X and Y be two compact figures in a metric space M (usually a Euclidean space); then DH(X,Y) is the infimum of dH(I(X),Y) along all isometries I of the metric space M to itself. This distance measures how far the shapes X and Y are from being isometric.
The Gromov–Hausdorff convergence is a related idea: we measure the distance of two metric spaces M and N by taking the infimum of dH(I(M),J(N)) along all isometric embeddings I:M→L and J:N→L into some common metric space L.
See also
References
- ^ R. Tyrrell Rockafellar, Roger J-B Wets, Variational Analysis, Springer-Verlag, 2005, ISBN 3540627723, ISBN 978-3540627722, pg.117.
- ^ Munkres, James; Topology (2nd edition). Prentice Hall, 1999. Pages 280--281.
- ^ [1] Completeness and Total Boundedness of the Hausdorff Metric
- ^ Barnsley, Michael (1993). Fractals Everywhere. Morgan Kaufmann. pp. Ch. II.6. ISBN 0120790696.
- ^ Hausdorff-Based Matching
- ^ P. Cignoni, C. Rocchini, R. Scopigno, "Metro: Measuring Error on Simplified Surfaces", Computer Graphics Forum, Volume 17, Number 2, June 1998, pp. 167-174
External links
- http://planetmath.org/encyclopedia/HausdorffMetric.html
- Completeness and Total Boundedness of the Hausdorff Metric (pdf)
- http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html
- Using MeshLab to measure difference between two surfaces A short tutorial on how to compute and visualize the Hausdorff distance between two triangulated 3D surfaces using the open source tool MeshLab.
- MATLAB code for Hausdorff distance: [2]

